Usando Python para resolver ODEs de circuitos elétricos: RL - Python

Usando Python para ODEs de circuitos elétricos: RL

Neste artigo explorarei a solução de circuitos elétricos utilizando Python. A solução analítica será encontrada utilizando SymPy enquanto a solução numérica será obtida com SciPy e Numpy.

Tratarei apenas do circuito RL da figura abaixo pois encontramos neste tipo de circuito apenas uma derivada. Estudaremos os casos para fontes DC e AC.

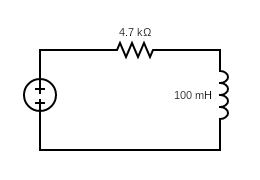
Para uma fonte DC de 5V o circuito é modelado pela seguinte equação diferencial

\[5 = 4700 i{\left(t \right)} + 0.0001 \frac{d}{d t} i{\left(t \right)}\]

Esse é um exemplo de Equação Diferencial Ordinária ou abreviadamente ODE cujas soluções podem ser analíticas ou numéricas. A solução analítica é a solução como conhecemos na escola ou a simples solução algébrica através de manipulação dos símbolos onde obteremos no final uma família de funções matemáticas em que podemos calcular o comportamento do circuito. Obter a solução analítica de uma ODE requer conhecimentos de cálculo 1 e 2 lecionados no nível superior, mas utilizando algum CAS (Computer Álgebra System) a solução pode ser encontrada rapidamente.

A solução numérica não manipula símbolos, utiliza-se de métodos interativos com tentativa e erros com um certo discernimento de para onde ir em busca da solução. Pode ser feito na mão ou mais adequadamente no computador.

Requerimentos

Como as soluções serão procuradas com Python precisaremos dos pacotes SymPy, Numpy, Matplotlib e SciPy que podem ser facilmente instalados utilizando o pip:

pip install sympy numpy matplotlib scipy

Em todos os arquivos os imports necessários e a cabeça do arquivo será este:

from sympy import *
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
%matplotlib inline

Versão analítica com SymPy

A solução analítica pode ser encontrada utilizando o módulo Sympy. É um módulo promissor, mas ainda está em um nível intermediário de maturidade. Não se compara em poder ao Maxima e ao Mathematica.

A solução analítica de uma ODE utilizando o Sympy é encontrada com o comando dsolve.

S = 5
R = 4700
L = 100e-6

t = Symbol('t')
v = Function('v')(t)
i = Function('i')(t)
    
eq = Eq(S,R*i+L*i.diff(t))
eq

O Sympy exibe em formato tex a equação acima como:

E como dito a solução analítica é encontrada pelo comando dsolve:

dsolve(eq)

cuja saída será:

Que é a função de $i$ em $t$ como desejamos. $C_1$ é uma constante que como toda equação diferencial e sistemas físicos que armazenam energia essa constante define a condição inicial da função, oras, temos um indutor no circuito que INICIALMENTE pode ter um campo magnético de valor 0 ou qualquer outro valor que iria interferir no início do circuito. Cabe a nós dizer qual é esse campo. Mas em geral começamos com condições iniciais com corrente zero, ou seja, $i(t=0) = 0$.

Versão numérica com SciPy e Numpy

Sim é muito Py. Pois este é poder do Python: Seus módulos! E as pessoas gostam de homenagear o Python colocando o Py no nome.

A solução numérica será encontrada utilizando o comando solve_ivp porém o correto agora é dizermos “as soluções” pois o que obteremos é uma tabela (List) com os valores numéricos de $i$ em $t$ que utilizaremos para visualizar o gráfico do comportamento da corrente no circuito.

O solve_ivp precisa que a equação esteja no formato

que no nosso caso então seria

e que esta equação esteja em forma de função Python, dessa forma definimos então a função circuito:

def circuito(t,i):
    return (5 -4700*i)/0.0001
    
tempo_maximo = 0.000001
t = np.linspace(0,tempo_maximo,1000)
sol = solve_ivp(circuito,[0,tempo_maximo],[0],method='RK45',t_eval=t)
plt.plot(sol.t,sol.y[0])

O primeiro parâmetro de solve_ivp é nossa função, o segundo o intervalo de tempo que a ODE será integrada e o [0] é o valor inicial e como foi dito antes a corrente no circuito inicialmente é zero, ou seja [0].

Tempo_maximo é crítico. Se um valor maior que o transitório do circuito for colocado não visualizaremos nada de útil, somente o estado estacionário do circuito. Se for muito pequeno veremos apenas o início do estado transitório que provavelmente será uma reta. Com os valores do programa o seguinte gráfico aparecerá:

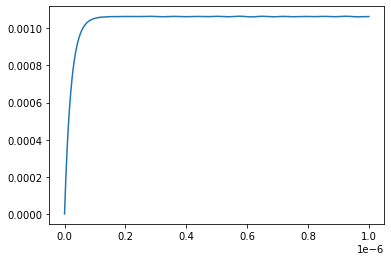
Como a fonte é contínua o gráfico se apresenta como o esperado. A corrente começa do zero e vai subindo gradativamente até que o indutor seja somente um curto-circuito e a corrente circulante seja a limitada pelo resistor.

Fonte de tensão senoidal

Um circuito de corrente contínua não nos oferece muito, vamos então usar uma fonte de tensão de 1Khz com Vp de 5V.

Solução analítica

S = 5*sin(t*(2*pi/(1/1000)))
R = 4700
L = 100e-6

t = Symbol('t')
v = Function('v')(t)
i = Function('i')(t)
    
eq = Eq(S,R*i+L*i.diff(t))
eq
dsolve(eq)

A única diferença é a mudança do S com a senoide provida pelo Seno do SymPy sin. As saídas serão então:

E a solução

Basicamente uma corrente não defasada com 1.06mA. Não entendi o outro cos de valor irrisório. Provavelmente o transitório inicial não seja uma composição pura do exponente e o seno, mas tenha algum componente que deforme a onda (Fourier).

Solução numérica

Já na solução numérica faremos maiores alterações.

def circuito(t,i):
    return (5*np.sin(t*(2*np.pi/0.0001)) -4700*i)/0.0001
    
tempo_maximo = 0.001
t = np.linspace(0,tempo_maximo,10000)
sol = solve_ivp(circuito,[0,tempo_maximo],[0],method='RK45',t_eval=t)
print(max(sol.y[0]),min(sol.y[0]))

plt.subplots(figsize=(15, 5))
plt.subplot(1, 2, 1)
plt.plot(sol.t,sol.y[0])
plt.subplot(1, 2, 2)
plt.plot(t,5*np.sin(t*(2*np.pi/0.0001)))

As alterações, além da fonte, foi o tempo que foi diminuído e exibimos o i máximo e mínimo como mostrado abaixo:

Nos gráficos abaixo o primeiro é a corrente do circuito encontrada pela solução numérica e o outro a tensão da fonte.

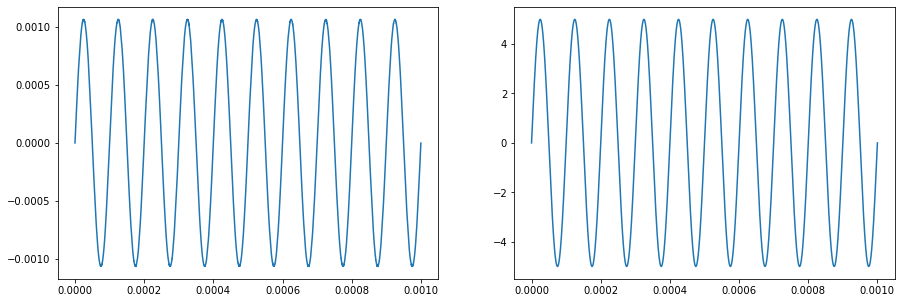
Os valores mínimos e máximos mostram uma corrente de 1.06mA que confere com a solução analítica obtida anteriormente.

Falstad

Vamos conferir com o simulador de circuitos do Falstad? Que aliás usa de muita solução numérica para simular o circuito.

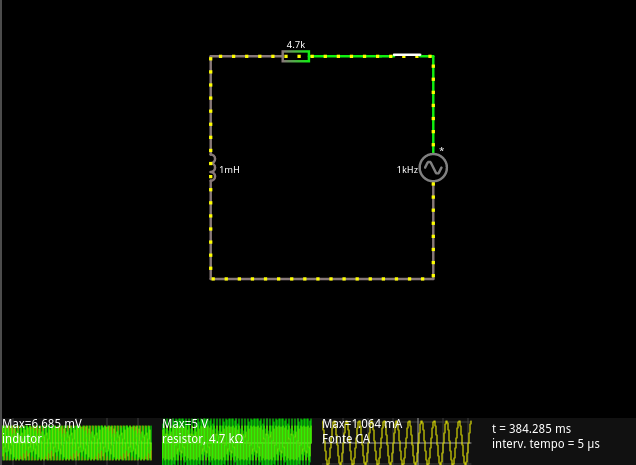
Como se pode ver no osciloscópio Fonte CA o Max=1.064mA novamente confere com os cálculos.

Link para o ipynb (Jupyter Notebook) deste post.

Espero que tenham gostado. Em breve novos posts!