Explorando o método Runge-Kutta em javascript

Bricando com equações diferenciais pelo método RK4

Equações diferenciais frequentemente surgem em modelos que estão associados a sistemas fisicos que armazenam energia, como por exemplo modelos matemáticos com molas, capacitores, pneumáticos, etc…. Entretanto encontrar a solução de uma equação diferencial não é trivial e muitas delas ainda não tem solução algébrica conhecida e por isso esses modelos matemáticos são um campo ativo de estudos. Todavia, não ter uma solução algébrica não impede de se obter seus valores, para tanto, métodos iterativos foram desenvolvidos com este fim.

Antes de ver alguns desses métodos em Java Script, abaixo você poderá explorar graficamente equações diferenciais resolvidas pelo método Runge-Kutta implementado aqui.

Utilize o formato javascript. O namespace Math pode ser suprimido.

Método de Euler

O primeiro método iterativo para solução de equações diferenciais foi criado pelo famoso matemático Euler; conhecido justamente como Método de Euler. Esse método faz apenas uma estimativa pontual do próximo valor e continua o processo a partir do último estimado. Como sua estimativa é fraca, erros se acumulam a cada iteração tornando inútil os valores por explodirem ou oscilarem. Entretanto por ser simples e fácil de implementar o método de Euler costuma ser exemplo de partida para estudos desses algoritmos.

Como toda equação diferencial que modela um sistema fisico esses métodos partem de uma condição inicial definida pelo usuário e a cada iteração uma estimativa do próximo valor é calculado repetindo-se o processo com o valor anterior.

Como este site é primariamente de eletrônica, vamos partir do exemplo do circuito RL abaixo que foi tema de artigo ¹ para começar a explorar alguns métodos:

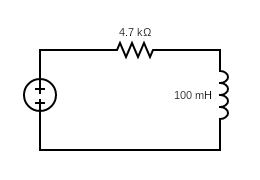
Para uma fonte DC de 5V o circuito é modelado pela seguinte equação diferencial

$5 = 4700 i{\left(t \right)} + 0.0001 \frac{d}{d t} i{\left(t \right)}$

Isolando $di(t) \over {dt}$ obtemos

${di(t) \over dt} = \frac{5 - 4700 * i(t)}{0.0001}$

O método de Euler é um método simples e didático. Primeiramente precisamos definir a função com a equaçao diferencial que será chamada a cada iteração para se obter o próximo valor. A função didt(t,i) definida abaixo é a equação do circuito RL visto acima. As condições iniciais são passadas pelos parametros y0 e x0. h é o passo que será dado a cada iteração, pense nisso como uma quantidade do tempo incrementado, e isso é importante, porque em um sistema rápido, digamos o circuito RL com indutância pequena, os valores acontecem rapidamente, enquanto em um modelo muito lento, como por exemplo modelos metereológicos, o tempo é da ordem de horas.

function didt(t, i) {
return (5 - 4700 * i) / 0.0001;
}

function Euler(y0, x0, h, final, f) {
const r = [];
let x = x0;
let y = y0;

r[0] = y;
while (x < final) {
    y = y + h * f(x, y);
    x = x + h;
    r.push(y);
}
return r;
}

r = Euler(0, 0, 0.0001, 0.1, didt);

console.log(r);

As condições iniciais do circuito no primeiro instante (t = 0) a corrente é igual a 0, logo y0 = 0 e x0 = 0. Como o algoritmo é iterativo cada passo representa uma quantidade no tempo, dessa forma h é a quantidade do passo dado no tempo. Como um circuito como esse se estabiliza rapidamente, h deverá ser da ordem dos micro segundos ou nano segundos. O parametro final informa ao algoritmo quando terminar. O método de Euler é puramente didático. Ele faz péssimas estimativas do próximo valor que vão se acumulando, retornando, então, valores irreais e oscilatórios. De fato no programa acima em poucas iterações os valores se tornam irreais e explosivos.

Método de Runge-Kutta

Amplamente utilizado, o método de Runge-Kutta converge adequadamente, não acumula muitos erros e tem poucas chances de oscilar. Em contraste ao método de Euler as estimativas são feitas através de média aritmética ponderada de 4 valores (K_n).

function didt(t, i) {
return (5 - 4700 * i) / 0.0001;
}

function RK(y0, x0, h, final, f) {
const r = [];
let x = x0;
let y = y0;
let k1, k2, k3, k4;

r.push(y);
while (x < final) {
    k1 = h * f(x, y);
    h2 = h / 2; // Uma pequena otimização
    k2 = h * f(x + h2, y + h2 * k1);
    k3 = h * f(x + h2, y + h2 * k2);
    k4 = h * f(x + h, y + h * k1);
    y = y + (h * (k1 + 2 * k2 + 2 * k3 + k4)) / 6;
    x = x + h;

    r.push(y);
}
return r;
}

r = RK(0, 0, 0.0001, 0.1, didt);

console.log(r);

Certamente o array pode ser descartado e os valores usados dinamicamente para plotar um gráfico ou apenas o valor final seja de interesse.