Como perdi uma placa por utilizar o estimador estatístico errado
Me envolvi em mais um projeto de inversor de frequência para motores trifásicos, onde fui novamente responsável por tudo: projeto, roteamento e programação. Quando chegou a hora de rotear a placa, era necessário usar uma fonte chaveada indicada pelo cliente (que posteriormente apresentou problemas).
Havia no circuito um capacitor de filtro 22uF - 400V, responsável pelo AC-DC.
O local onde este capacitor iria ficar era apertado e não era um dos padrões que eu estava acostumado. Em geral, nesses projetos, ou eu roteava capacitores de até 36V, ou os já conhecidos capacitores de 1000uF - 250V, para os quais eu sempre deixava 35mm de diâmetro — e às vezes ainda sobrava espaço.
Então qual era o diâmetro desse desconhecido 22uF - 400V?
Inferência estatística
Quando estamos diante de um parâmetro numérico desconhecido de algo que apresenta variação e precisamos estimar esse valor, estamos lidando com uma inferência estatística. Isso acontece na vida o tempo todo, mas sabemos que não há especialistas em estatística por aí — na verdade, nem podemos admitir que haja muitas pessoas que conheçam matemática. Ainda assim, as pessoas têm alguma forma de saber esse valor desconhecido, seja por intuição, experiência ou puro chute.
No meu caso, entrei no site da Mouser e, utilizando os filtros Capacitores eletrolíticos, 400V e 22uF, cheguei aos seguintes valores:
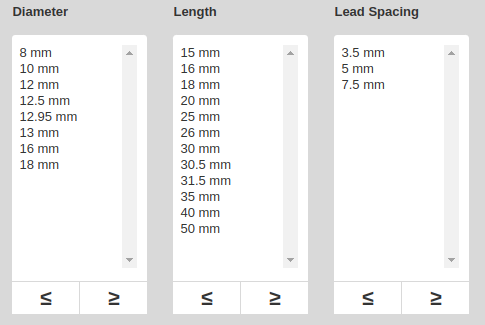
Resultado da pesquisa de Capacitor Eletrolítico 22uF 400V na Mouser
Veja só… de 8mm a 18mm de diâmetro. Só pode ser brincadeira?!
Qual valor usar?
Clicando em cada opção do listbox do site, aparece em cima a quantidade de ofertas, o que me permitiu montar uma tabela de frequências, mostrada abaixo:
| Tamanho | fi (Ofertas) | fr |
|---|---|---|
| 8 mm | 4 | 0,044 |
| 10 mm | 11 | 0,122 |
| 12 mm | 1 | 0,011 |
| 12,5 mm | 42 | 0,466 |
| 12,95 mm | 1 | 0,011 |
| 13 mm | 7 | 0,077 |
| 16 mm | 19 | 0,211 |
| 18 mm | 5 | 0,055 |
| 90 | 1,0 |
A distribuição das ofertas indicava que o diâmetro mais frequente era 12,5 mm, correspondendo a 46,6% das opções disponíveis. Com base nesse dado, decidi usar esse valor para o layout da minha placa.
Mas, para minha surpresa, o montador responsável pelas placas do cliente utilizou um capacitor bem maior, o que fez com que ele precisasse ficar “aéreo”, praticamente inviabilizando a placa.
O erro estava na métrica usada para a inferência. A moda é um bom estimador em muitas situações, mas, nesse caso, não levou em conta que a distribuição dos valores era assimétrica e que fabricantes podem priorizar determinados tamanhos com base em fatores não refletidos apenas na frequência das ofertas.
Talvez uma abordagem mais conservadora teria sido considerar o percentil superior ou reservar um espaço extra com base na variabilidade dos dados.
